BinaryMuseGAN
Background
Stochastic and Deterministic Binary Neurons
Binary neurons (BNs) are neurons that output binary-valued predictions. In this work, we consider two types of BNs:
-
Deterministic Binary Neurons (DBNs) act like neurons with hard thresholding functions as their activation functions. We define the output of a DBN for a real-valued input x as:
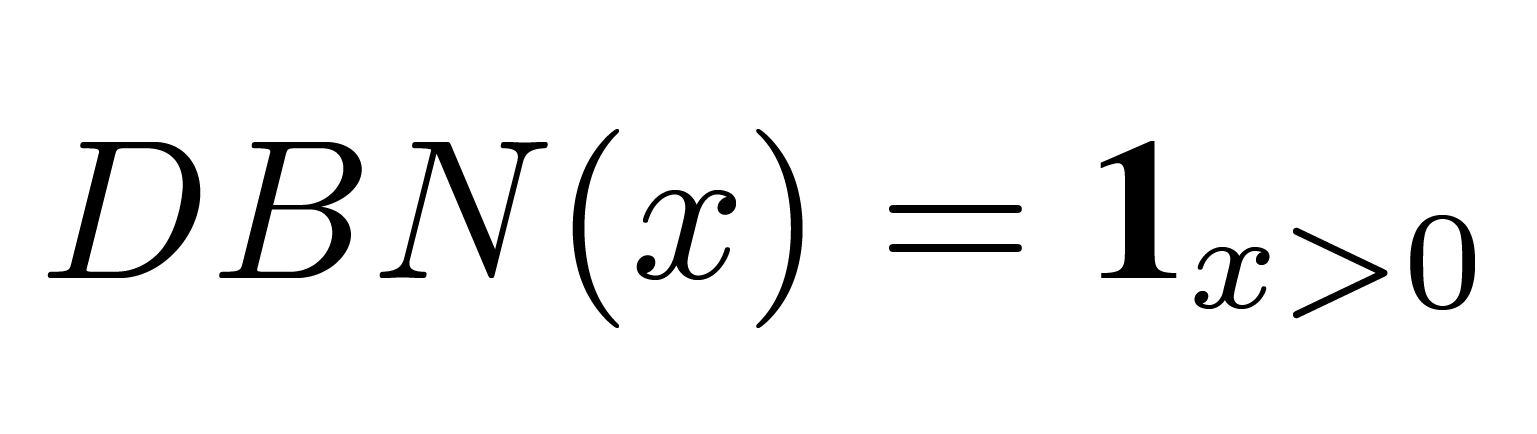 where 1(·) is the indicator function.
where 1(·) is the indicator function. -
Stochastic Binary Neurons (SBNs) binarize a real-valued input x according to a probability, defined as:
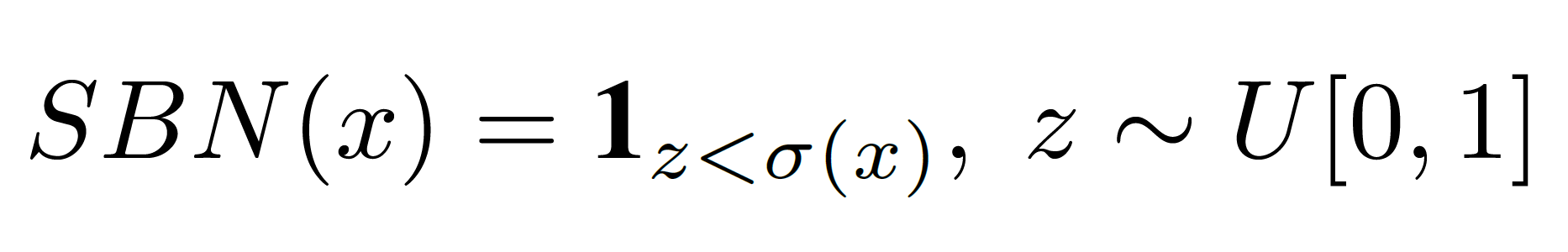 where σ(·) is the logistic sigmoid function and U[0, 1] denotes
an uniform distribution.
where σ(·) is the logistic sigmoid function and U[0, 1] denotes
an uniform distribution.
Straight-through Estimator
Computing the exact gradients for either DBNs or SBNs, however, is intractable, for doing so requires the computation of the average loss over all possible binary samplings of all the BNs, which is exponential in the total number of BNs.
A few solutions have been proposed to address this issue [1, 2]. In this work, we resort to the sigmoid-adjusted straight-through (ST) estimator when training networks with DBNs and SBNs. The ST estimator is first proposed in [3], which simply treats BNs as identify functions and ignores their gradients. The sigmoid-adjusted ST estimator is a variant which multiply the gradients in the backward pass by the derivative of the sigmoid function.
By replacing the non-differentiable functions, which are used in the forward pass, by differentiable functions (usually called the estimators) in the backward pass, we can then train the whole network with back propagation.
References
-
Silviu Pitis, “Binary Stochastic Neurons in Tensorflow,” 2016. Blog post on R2RT blog. link
-
Yoshua Bengio, Nicholas Léonard, and Aaron C. Courville, “Estimating or propagating gradients through stochastic neurons for conditional computation,” arXiv preprint arXiv:1308.3432, 2013.
-
Geoffrey Hinton, “Neural networks for machine learning - using noise as a regularizer (lecture 9c)”, 2012. Coursera, video lecture. video